BST Level Order Traversal
Source: Hacker rank
Task
A level-order traversal, also known as a breadth-first search, visits each level of a tree's nodes from left to right, top to bottom. You are given a pointer, root, pointing to the root of a binary search tree. Complete the levelOrder function provided in your editor so that it prints the level-order traversal of the binary search tree.
Hint: You'll find a queue helpful in completing this challenge.
Input Format
The locked stub code in your editor reads the following inputs and assembles them into a BST: The first line contains an integer,T (the number of test cases).
The T subsequent lines each contain an integer, data, denoting the value of an element that must be added to the BST.
Output Format
Print the data value of each node in the tree's level-order traversal as a single line of N space-separated integers.
Sample Input
6
3
5
4
7
2
1
Sample Output
3 2 5 1 4 7
Explanation
The input forms the following binary search tree:
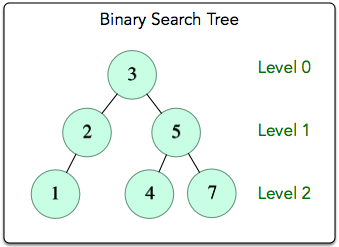
We traverse each level of the tree from the root downward, and we process the nodes at each level from left to right. The resulting level-order traversal is 3->2->5->1->4->7, and we print these data values as a single line of space-separated integers.
My solution:
C#:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 | using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks; namespace BSTLevelOrderTraversal { class Node { public Node left, right; public int data; public Node(int data) { this.data = data; left = right = null; } } class Program { static void levelOrder(Node root) { //Write your code here //Apply Breadth-first search Queue<Node> queue = new Queue<Node>(); queue.Enqueue(root); while(queue.Count()!=0) { Node no = queue.Dequeue(); //visit node Console.Write(no.data + " "); //enqueue each node son if (no.left != null) queue.Enqueue(no.left); if (no.right != null) queue.Enqueue(no.right); } } static Node insert(Node root, int data) { if (root == null) { return new Node(data); } else { Node cur; if (data <= root.data) { cur = insert(root.left, data); root.left = cur; } else { cur = insert(root.right, data); root.right = cur; } return root; } } static void Main(String[] args) { Node root = null; int T = Int32.Parse(Console.ReadLine()); while (T-- > 0) { int data = Int32.Parse(Console.ReadLine()); root = insert(root, data); } levelOrder(root); Console.ReadKey(); } } } |